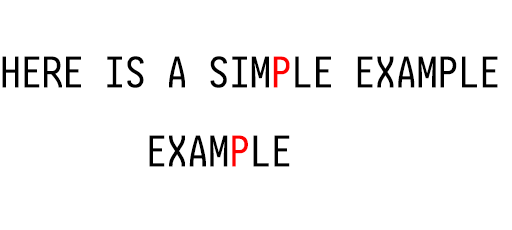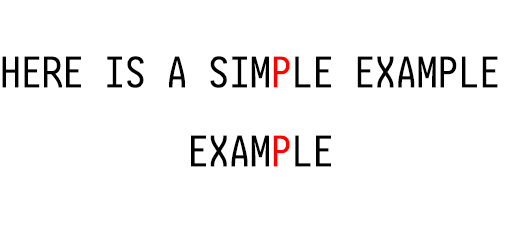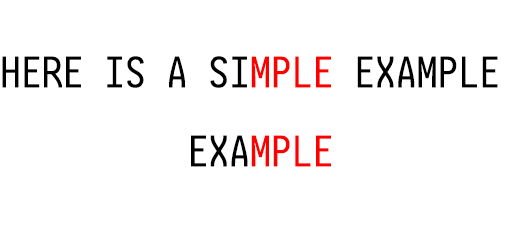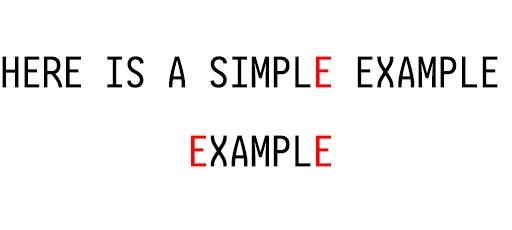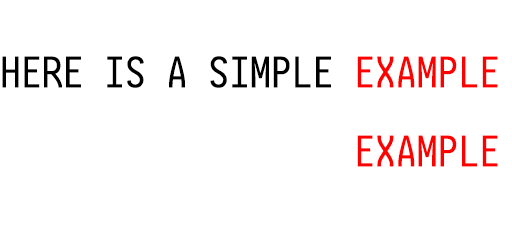Boyer-Moore字符串查找

---

字符串查找一直是编程的重点内容。前文我介绍了正则表达式的应用，然而在实际中，最为广泛应用的是一个叫做 Boyer-Moore 的字符串查找算法。

---

应用

这算法的来历我就不讲了，有兴趣的自己百度。
其被广泛应用于各大文本编辑器内，如：

由此可见该种算法的普适和高效。

实现

Boyer-Moore 算法和普通匹配字符串的方式不同，它用了更为巧妙的变化，使得匹配次数大大缩减。

匹配方向

Boyer-Moore算法 采取从后往前匹配的规则。
如下图所示，从匹配字符串的最后一个字符开始向前匹配。

坏字符规则

我们发现 S 和 E 无法匹配，且 S 并不存在于 EXAMPLE 内。所以将整个匹配字符串向前移动 7 个单位。
可以称 S 为所谓坏字符。

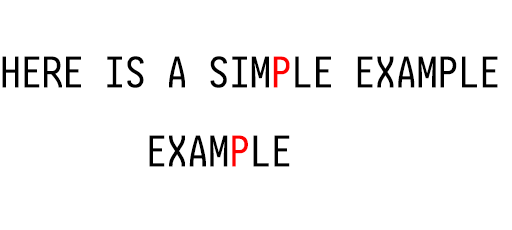
随后继续上述过程，发现 P 和 E 无法匹配。但此时 P 存在于 EXAMPLE 内，所以将两个 P 对齐。

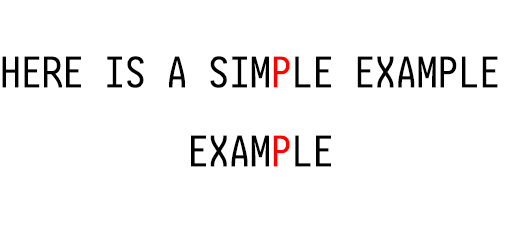
通过上边两次移动，我们可以发现一个事实：
匹配字符串移动距离 = 坏字符匹配位置 - 第一次坏字符出现位置。

当匹配字符串内不存在坏字符，令值为 -1 。

利用上述公式，可以计算出移动的位置：

第一次移动距离为：$Length1 = 6 - (-1) = 7$
第二次移动距离为：$Length2 = 6 - 4 = 2$
上述公式就是所谓坏字符规则。

好后缀规则

继续匹配，此时可以发现 MPLE 均已经匹配。若是用坏字符规则，会移动 3 个单位。
其中 MPLE 被称作好后缀。

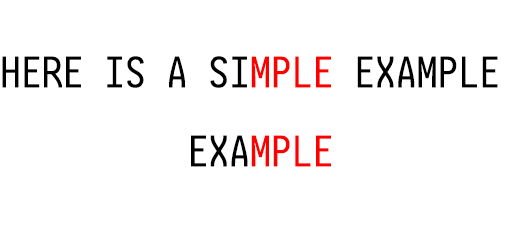
但此时还有更好的移动方式，可以直接移动 6 个单位。
这里用到了好后缀规则。类似于坏字符规则，其公式为:
匹配字符串移动距离 = 好后缀匹配位置 - 匹配字符串头部好后缀出现的位置。

当匹配字符串头部不存在好后缀时，令其值为 -1 。

如下图，E 就是计算用的好后缀。

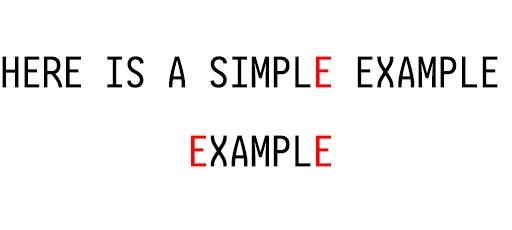
利用上述公式，可以计算出移动的位置：$Length = 6 - 0 = 6$

然后用坏字符规则，便可匹配字符串。

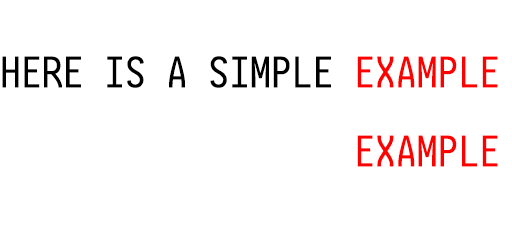
综合规则

两大规则为 Boyer-Moore 算法提供了匹配的依据。为了达成最高效的匹配，必须尽可能的减少匹配次数。
故匹配字符串每次实际移动距离为:
$Length = Max\{\ BadChar(\ ),\ GoodSuffix(\ )\ \} $。

代码

具体实现代码如下

class BoyerMooreMatch
{
    public static (int Start, int End) Match(string str, string pattern)
    {
        int index = pattern.Length - 1;
        int indexReturn = -1;
        string suffix;
        char badChar = '\0';
        int badCharIndex = 0;
        while (index < str.Length)
        {
            suffix = "";
            for (int i = pattern.Length - 1, j = index; i >= 0; i--, j--)
            {
                if (str[j] == pattern[i])
                    suffix += pattern[i];
                else
                {
                    badChar = str[j];
                    badCharIndex = i;
                    break;
                }
            }

            suffix = FlipString(suffix);
            if (suffix == pattern)
            {
                indexReturn = index;
                if (suffix.Length > 1)
                    indexReturn -= suffix.Length - 1;
                break;
            }

            if (suffix.Length != 0)
                index += Math.Max(GetBadCharNumber(pattern, badCharIndex, badChar), GetGoodSuffixNum(pattern, suffix));
            else
                index += GetBadCharNumber(pattern, badCharIndex, badChar);
        }

        return (indexReturn, index);
    }

    private static int GetBadCharNumber(string pattern, int index, char c)
    {
        int start = -1;
        int end = index;

        for (int i = end - 1; i >= 0; i--)
        {
            if (pattern[i] == c)
            {
                start = i;
                break;
            }
        }

        return end - start;
    }

    private static int GetGoodSuffixNum(string pattern, string suffix)
    {
        int start = -1;
        int end = pattern.Length - 1;

        for (int i = suffix.Length - 1, j = 0; i >= 0; i--, j++)
        {
            if (pattern[j] != suffix[i])
                break;
            start++;
        }

        return end - start;
    }

    private static string FlipString(string str)
    {
        char[] chars = str.ToCharArray();
        Array.Reverse(chars);
        return new string(chars);
    }
}

利用元组，可以返回匹配区间。

---